Materi Matematika SD Kelas V Jenis-Jenis Bangun Datar dan Rumusnya
Bangun Datar
Bangun datar adalah sebuah obyek benda dua dimensi yang dibatasi oleh garis-garis lurus atau garis lengkung. Karena bangun datar merupakan bangun dua dimensi, maka hanya memiliki ukuran panjang dan lebar oleh sebab itu maka bangun datar hanya memiliki luas dan keliling.
Sebelum membahas mengenai jenis-jenis bangun datar, berikut ini ada beberapa istilah yang sering dipakai dalam materi bangun datar :
1. Sisi
Sisi adalah garis pembatas dari suatu bidang datar.
Berikut ini ada contoh sisi dari persegi :
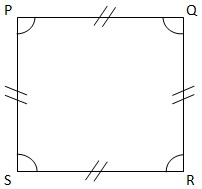
Dari gambar persegi diatas, yang dimaksud dengan sisi adalah garis SR, RQ, QP dan PS.
2. Sudut
Sudut adalah besaran rotasi antara dua garis, antara dua bidang, atau antara garis dengan bidang.
Berikut ini ada contoh sudut dari persegi :

Dari gambar tersebut terlihat bahwa sudut yang terdapat dalam persegi adalah sudut A, B, C dan D.
3. Diagonal Bidang
Diagonal Bidang adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada setiap bidang.
Berikut ini ada contoh diagonal bidang dari persegi :

Dari gambar diatas, terlihat bahwa diagonal bidang dari persegi adalah garis AC dan garis BD.
4. Simetri Lipat
Simetri lipat adalah suatu proses pelipatan bidang datar menjadi dua bagian dengan bentuk dan ukuran yang sama pada setiap bagiannya. Garis yang menjadi garis lipatan tersebut dinamakan garis simetri atau sumbu simetri. Beberapa bidang datar ada yang memiliki simetri lipat, ada pula yang tidak. Banyaknya jumlah cara lipatan yang terjadi menunjukan banyaknya simetri putar bangun tersebut.
Berikut ini ada contoh garis yang menunjukan simetri lipat :

5. Simetri Putar
Simetri putar adalah Suatu proses memutar bangun datar sebanyak kurang dari satu putaran penuh sehingga hasil perputaran tersebut tepat pada bentuk semula bangun tersebut. Banyaknya jumlah putaran yang terjadi menunjukan banyaknya simetri putar bangun tersebut.
Berikut ini ada contoh yang menunjukan proses simetri putar dari sebuah segitiga sama sisi :

Beberapa jenis bangun datar dan juga rumus untuk mencari luas dan kelilingnya :
1. Persegi
Bentuk umum dari sebuah persegi adalah sebagai berikut :

Sifat-sifat Persegi
Memiliki empat sisi serta empat titik sudut
Memiliki dua pasang sisi yang sejajar serta sama panjang
Keempat sisinya sama panjang
Keempat sudutnya sama besar yaitu 90° ( sudut siku-siku )
Memiliki empat buah simetri lipat
Memiliki empat simetri putar
Rumus luas persegi :
Luas = sisi x sisi
Rumus keliling persegi :
Keliling = 4 x sisi
2. Persegi Panjang
Bentuk umum dari sebuah persegi panjang adalah sebagai berikut :

Sifat-sifat Persegi Panjang
Memiliki empat sisi serta empat titik sudut
Memiliki dua pasang sisi sejajar yang berhadapan dan sama panjang
Keempat sudutnya sama besar yaitu 90° ( sudut siku-siku )
Memiliki dua diagonal yang sama panjang
Memiliki dua buah simetri lipat
Memiliki dua simetri putar
Rumus luas persegi panjang :
Luas = panjang x lebar
Rumus keliling persegi panjang :
Keliling = 2 x ( panjang + lebar )
3. Jajar Genjang
Bentuk umum dari sebuah jajar genjang adalah sebagai berikut :

Sifat-sifat Jajar Genjang
Memiliki empat sisi dan empat titik sudut
Memiliki dua pasang sisi yang sejajar dan sama panjang
Memiliki dua buah sudut tumpul dan dua buah sudut lancip
Sudut yang berhadapan sama besar
Diagonal yang dimiliki tidak sama panjang
Tidak memiliki simetri lipat
Memiliki dua simetri putar
Rumus luas jajar genjang :
Luas = alas x tinggi
Rumus keliling jajar genjang :
Keliling = (2 x alas) + (2 x tinggi)
4. Belah Ketupat
Bentuk umum dari sebuah belah ketupat adalah sebagai berikut :

Sifat-sifat Belah Ketupat
Memiliki empat buah sisi dan empat buah titik sudut
Keempat sisinya sama panjang
Dua pasang sudut yang berhadapan sama besar
Diagonalnya berpotongan tegak lurus
Memiliki dua buah simetri lipat
Memiliki simetri putar tingkat dua
Rumus Luas Belah Ketupat :
Luas = 1/2 x diagonal 1 x diagonal 2
Rumus Keliling Belah Ketupat :
Keliling = jumlah panjang sisi belah ketupat
5. Trapesium
Bentuk umum dari sebuah trapesium adalah sebagai berikut :

Sifat-sifat Trapesium
Memiliki empat sisi dan empat titik sudut
Memiliki sepasang sisi yang sejajar tetapi tidak sama panjang
Sudut-sudut diantara sisi sejajar besarnya 180°
Rumus Luas Trapesium:
Luas =
Rumus Keliling Trapesium :
Keliling = jumlah semua sisi trapesium.
6. Layang-Layang
Bentuk umum dari sebuah layang-layang adalah sebagai berikut :

Sifat-sifat Layang-Layang
Memiliki empat sisi dan empat titik sudut
Memiliki dua pasang sisi yang sama panjang
Memiliki dua sudut yang sama besarnya
Diagonalnya berpotongan tegak lurus
Salah satu diagonalnya membagi diagonal yang lain sama panjang
Memiliki satu simetri lipat
Rumus Luas Layang-Layang :
Luas = 1/2 x diagonal 1 x diagonal 2
Rumus Keliling Layang-Layang :
Keliling = Jumlah semua sisi layang-layang
7. Segitiga
Bentuk umum dari sebuah segitiga adalah sebagai berikut :

Sifat-sifat Segitiga
Mempunyai 3 sisi dan tiga titik sudut
Jumlah ketiga sudutnya 180
Rumus Luas Segitiga :
Luas = 1/2 x alas x tinggi
Rumus Keliling Segitiga :
Keliling = jumlah panjang sisi segitiga
8. Lingkaran
Bentuk umum dari sebuah lingkaran adalah sebagai berikut :

Sifat-sifat Lingkaran
Mempunyai satu sisi
Memiliki simetri putar dan simetri lipat tak berhingga
Rumus Luas Lingkaran:
Luas = x
x 
Rumus Keliling Belah Ketupat :
Keliling = jumlah panjang sisi belah ketupat
Demikian jenis-jenis dari bangun ruang beserta sifat dan rumusnya.
Bangun datar adalah sebuah obyek benda dua dimensi yang dibatasi oleh garis-garis lurus atau garis lengkung. Karena bangun datar merupakan bangun dua dimensi, maka hanya memiliki ukuran panjang dan lebar oleh sebab itu maka bangun datar hanya memiliki luas dan keliling.
Sebelum membahas mengenai jenis-jenis bangun datar, berikut ini ada beberapa istilah yang sering dipakai dalam materi bangun datar :
1. Sisi
Sisi adalah garis pembatas dari suatu bidang datar.
Berikut ini ada contoh sisi dari persegi :

Dari gambar persegi diatas, yang dimaksud dengan sisi adalah garis SR, RQ, QP dan PS.
2. Sudut
Sudut adalah besaran rotasi antara dua garis, antara dua bidang, atau antara garis dengan bidang.
Berikut ini ada contoh sudut dari persegi :

Dari gambar tersebut terlihat bahwa sudut yang terdapat dalam persegi adalah sudut A, B, C dan D.
3. Diagonal Bidang
Diagonal Bidang adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada setiap bidang.
Berikut ini ada contoh diagonal bidang dari persegi :
Dari gambar diatas, terlihat bahwa diagonal bidang dari persegi adalah garis AC dan garis BD.
4. Simetri Lipat
Simetri lipat adalah suatu proses pelipatan bidang datar menjadi dua bagian dengan bentuk dan ukuran yang sama pada setiap bagiannya. Garis yang menjadi garis lipatan tersebut dinamakan garis simetri atau sumbu simetri. Beberapa bidang datar ada yang memiliki simetri lipat, ada pula yang tidak. Banyaknya jumlah cara lipatan yang terjadi menunjukan banyaknya simetri putar bangun tersebut.
Berikut ini ada contoh garis yang menunjukan simetri lipat :

5. Simetri Putar
Simetri putar adalah Suatu proses memutar bangun datar sebanyak kurang dari satu putaran penuh sehingga hasil perputaran tersebut tepat pada bentuk semula bangun tersebut. Banyaknya jumlah putaran yang terjadi menunjukan banyaknya simetri putar bangun tersebut.
Berikut ini ada contoh yang menunjukan proses simetri putar dari sebuah segitiga sama sisi :

Beberapa jenis bangun datar dan juga rumus untuk mencari luas dan kelilingnya :
1. Persegi
Bentuk umum dari sebuah persegi adalah sebagai berikut :

Sifat-sifat Persegi
Memiliki empat sisi serta empat titik sudut
Memiliki dua pasang sisi yang sejajar serta sama panjang
Keempat sisinya sama panjang
Keempat sudutnya sama besar yaitu 90° ( sudut siku-siku )
Memiliki empat buah simetri lipat
Memiliki empat simetri putar
Rumus luas persegi :
Luas = sisi x sisi
Rumus keliling persegi :
Keliling = 4 x sisi
2. Persegi Panjang
Bentuk umum dari sebuah persegi panjang adalah sebagai berikut :

Sifat-sifat Persegi Panjang
Memiliki empat sisi serta empat titik sudut
Memiliki dua pasang sisi sejajar yang berhadapan dan sama panjang
Keempat sudutnya sama besar yaitu 90° ( sudut siku-siku )
Memiliki dua diagonal yang sama panjang
Memiliki dua buah simetri lipat
Memiliki dua simetri putar
Rumus luas persegi panjang :
Luas = panjang x lebar
Rumus keliling persegi panjang :
Keliling = 2 x ( panjang + lebar )
3. Jajar Genjang
Bentuk umum dari sebuah jajar genjang adalah sebagai berikut :

Sifat-sifat Jajar Genjang
Memiliki empat sisi dan empat titik sudut
Memiliki dua pasang sisi yang sejajar dan sama panjang
Memiliki dua buah sudut tumpul dan dua buah sudut lancip
Sudut yang berhadapan sama besar
Diagonal yang dimiliki tidak sama panjang
Tidak memiliki simetri lipat
Memiliki dua simetri putar
Rumus luas jajar genjang :
Luas = alas x tinggi
Rumus keliling jajar genjang :
Keliling = (2 x alas) + (2 x tinggi)
4. Belah Ketupat
Bentuk umum dari sebuah belah ketupat adalah sebagai berikut :

Sifat-sifat Belah Ketupat
Memiliki empat buah sisi dan empat buah titik sudut
Keempat sisinya sama panjang
Dua pasang sudut yang berhadapan sama besar
Diagonalnya berpotongan tegak lurus
Memiliki dua buah simetri lipat
Memiliki simetri putar tingkat dua
Rumus Luas Belah Ketupat :
Luas = 1/2 x diagonal 1 x diagonal 2
Rumus Keliling Belah Ketupat :
Keliling = jumlah panjang sisi belah ketupat
5. Trapesium
Bentuk umum dari sebuah trapesium adalah sebagai berikut :

Sifat-sifat Trapesium
Memiliki empat sisi dan empat titik sudut
Memiliki sepasang sisi yang sejajar tetapi tidak sama panjang
Sudut-sudut diantara sisi sejajar besarnya 180°
Rumus Luas Trapesium:
Luas =
Rumus Keliling Trapesium :
Keliling = jumlah semua sisi trapesium.
6. Layang-Layang
Bentuk umum dari sebuah layang-layang adalah sebagai berikut :

Sifat-sifat Layang-Layang
Memiliki empat sisi dan empat titik sudut
Memiliki dua pasang sisi yang sama panjang
Memiliki dua sudut yang sama besarnya
Diagonalnya berpotongan tegak lurus
Salah satu diagonalnya membagi diagonal yang lain sama panjang
Memiliki satu simetri lipat
Rumus Luas Layang-Layang :
Luas = 1/2 x diagonal 1 x diagonal 2
Rumus Keliling Layang-Layang :
Keliling = Jumlah semua sisi layang-layang
7. Segitiga
Bentuk umum dari sebuah segitiga adalah sebagai berikut :

Sifat-sifat Segitiga
Mempunyai 3 sisi dan tiga titik sudut
Jumlah ketiga sudutnya 180
Rumus Luas Segitiga :
Luas = 1/2 x alas x tinggi
Rumus Keliling Segitiga :
Keliling = jumlah panjang sisi segitiga
8. Lingkaran
Bentuk umum dari sebuah lingkaran adalah sebagai berikut :

Sifat-sifat Lingkaran
Mempunyai satu sisi
Memiliki simetri putar dan simetri lipat tak berhingga
Rumus Luas Lingkaran:
Luas =
Rumus Keliling Belah Ketupat :
Keliling = jumlah panjang sisi belah ketupat
Demikian jenis-jenis dari bangun ruang beserta sifat dan rumusnya.
Tidak ada komentar:
Posting Komentar